基于 BP 神经网络的识别手写体数字 - 神经网络基础
(基于 BP 神经网络的识别手写体数字, Part 1)
前言
上个月,公司内部举办了机器学习比赛,内容是识别手写体数字。
我提交的方案参考 Michael Nielsen。以下大部分内容也参考了他写的深度学习在线电子书。
人类视觉系统其实非常神奇,恐怕自己都没意识到,考虑以下的手写数字:
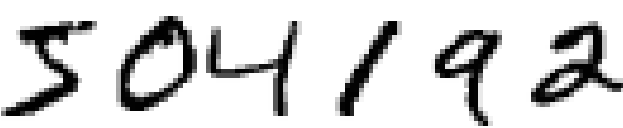
大部分人能够识别出数字为 504192。人脑每一半球都有着近 1.4 亿个神经元,之间有数以百亿的连接,能够进行复杂的图像处理。相当于每个人随身携带了一台超级计算机,数百万年的进化让该系统训练有素,能够适应并理解视觉世界。
当真正开始编写程序时,就会意识到手写数字中复杂之处。在教小孩认数字 9 时,可能会 “这个数字顶上有个圈,右下角有个垂直的竖线。。”,或者你给他看一眼写的 9,他就能学会了。但这些步骤根本无法用传统的算法来描述,因为一个手写数字有着无限的细节。
神经网络算法则用另一种方法来解决问题。首先,会准备如下的训练数据,

然后,系统便以此为基础学习。换句话说,神经网络能够使用这些训练数据自动推导出识别手写数字的规则。并且,训练集越多,神经网络准确率越高。所以虽然上图只展示了 100 个数字,但如果有上百万个训练集的话,我们的手写数字识别器效果会更好。
神经网络是一个简单易实现的算法,不会超过 100 行代码。我们也会在将来探讨更为复杂的深度学习算法。
感知器 Perceptron
什么是神经网络?我们从感知器说起。
感知器是上世纪 50 年代,Frank Rosenblatt 受 Warren McCulloch 和 Walter Pitts 工作的启发,所提出的概念。如今,其他的人工神经元模型更常用,最广泛的是 sigmoid 神经元。现在先让我们看看感知器模型,它将帮助我们了解为什么 sigmoid 神经元更受欢迎。
感知器如何工作呢?一个感知器有多个二进制输入,$x_1, x_2, ...$,并只有一个二进制的输出:
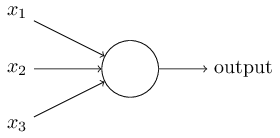
这个例子中,感知器有三个输入,$x_1, x_2, x_3$。通常输入数目由需要而定。Rosenblatt 给每一个输入引入一个权重,$w_1, w_2, ...$,在输出增加一个阈值,超过阈值时才会输出 1,以下为输出与输入的关系:
\begin{equation}
output = \left\{\begin{aligned}
0, \sum_jw_jx_j \leq threshold \\
1, \sum_jw_jx_j > threshold
\end{aligned}\right.
\end{equation}
这个简单的公式就是感知器的工作原理!
下面给出一个简单的模型,虽然不是实际例子,但易于理解。假设周末即将来临,你听说自己所在的城市会举办奶酪节。你太喜欢奶酪了,但还是得考虑一下周末的天气情况。你将根据下面三个因素来做决定:
- 天气怎样?
- 你的女朋友和你一起去吗?
- 节日举办地驾车方便吗?
将这三种因素量化成二进制数 $x_1, x_2, x_3$。比如如果天气好,则 $x_1=1$,否则为 $x_1=0$。其他三种因素同理。现在假设你太喜欢奶酪了,以至于女朋友和交通不遍都不太影响你,但你又怕糟糕的天气弄脏衣服。我们可以将感知器设计为:天气权重$w_1=6$,女朋友权重 $w_2=2$ 和交通状况权重 $w_3=2$。可以看到天气占了很大的权重。最后将感知器阈值设为 5 便得到了我们需要的决策模型。一旦天气不好,感知器输出为 0,天气晴朗就输出 1。而女朋友同去与否和交通状况都没法影响感知器输出。
通过改变加权系数和阈值,便能得到不同的决策系统。比如将阈值调整为 3,这样女朋友就对你很重要啦,她要是想去,天气再糟你也得跟着一起受罪。
虽然感知器并不是人类决策系统的完整模型,但其能对各种条件做加权。而且似乎越复杂的网路越能做出微妙的决策:
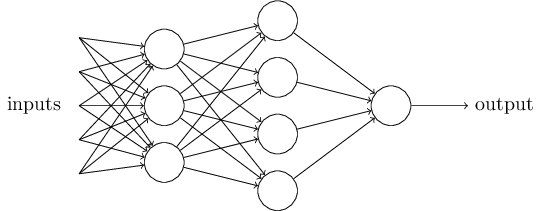
在这个网络中,第一列感知器 - 我们也称作感知器第一层,只是简单地对输入做加权。而第二层感知器则对第一层决策的结果再一步加权,做出更复杂更抽象的决定。同样还可以增加神经网络的层数来作出更复杂的决定。
顺便提一句,上述定义中,感知器只有一个输出,但是上述网络似乎有多个输出。事实上,这仍然是单输出系统,只是单个输出连接到了下一层的多个输入而已。
让我们来简化一下感知器的数学表达式,原来的判断条件 $\sum_jw_jx_j > threshold$ 略显累赘。首先用点积形式简化,记 $w \cdot x \equiv \sum_j w_j x_j$,其中 $w$ 是权重向量,$x$ 是输入向量。然后将阈值移到不等式左边,并用偏移的概念取代它,记 $b \equiv - threshold$。感知器规则可重写如下:
\begin{equation}
output = \left\{\begin{aligned}
0, w \cdot x + b \leq 0 \\
1, w \cdot x + b > 0
\end{aligned}\right.
\end{equation}
偏移的概念可用来度量感知器的“兴奋”程度,假如偏移值很大,那么很小的输入就会在输出端反应出来。但若偏移值很小,则说明感知器比较“迟钝”,输入很大时,输出才有变化。接下来的文章中,都会使用偏移而不是阈值的概念。
sigmoid 神经元
自学习的 idea 听起来太棒了。如何为神经网络设计算法呢?假设我们的神经网络全部由感知器构成,输入为手写体数字扫描图的每一个原始像素点。我们希望神经网络能够自调整权重和偏移值,从而能对手写数字准确分类。为了解自学习过程,我们来做一个思想实验,假设我们在权重或偏移做一个小的改变,我们期望输出也会有相应小的变化:
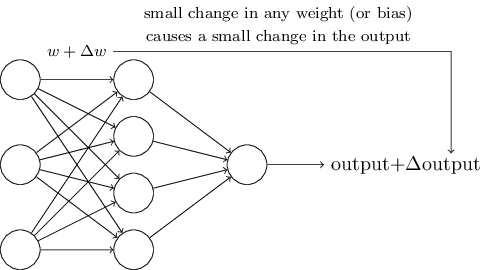
比如神经网络错误地将数字 9 认为为数字 8,我们就可以对参数做微调(可能某个人写的 9 像 8),修正输出,不断重复上述过程,从而使输出符合我们的预期。
实际中,由感知器组成的神经网络并不如所愿。由于感知器的输出不是连续的,0 到 1 是阶跃变化,上述参数的微调往往带来输出的剧烈变化。这下便导致自学习过程完全不可控,有时一点小小的噪声,输出就天壤之变。
针对这个问题,我们可以换用 sigmoid 神经元。sigmoid 神经元和感知器是类似的,但输出是连续且变化缓慢的。这个微小的不同使神经网络算法化成为了可能。
好,让我来描述一下 sigmoid 神经元。其结构和感知器一样:
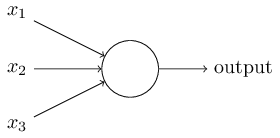
同样有输入 $x_1, x_2, ...$。不同是,输入可以取 0 到 1 之间的任何值,比如 0.638。sigmoid 对每一个输入有一个权重,$w_1, w_2, ...$,以及全局的偏移 $b$。但是 sigmoid 的输出不再限于 0 和 1,而是
\begin{equation}
\sigma(z) \equiv \frac{1}{1+e^{-z}}.
\end{equation}
将 $z=w \cdot x+b$ 展开,可得
\begin{equation} \frac{1}{1+\exp(-\sum_j w_j x_j-b)}. \label{eq4} \end{equation}
初看上去,sigmoid 神经元似乎与感知器有着天壤之别,其代数表达式也显得晦涩难懂。然而他们之间是有很多相似之处的。
假设当 $z\equiv w \cdot x + b$ 趋向于正无穷,则 $e^{-z}\approx 0$ 和 $\sigma(z) \approx 1$。换句话说,当输入很大时,sigmoid 神经元的输出趋向于 1,这和感知器是一样的。相反的,当 $z\equiv w \cdot x + b$ 趋向于负无穷,则 $e^{-z} \rightarrow \infty$,且 $\sigma(z) \approx 0$。这和感知器又是一样的。只有当输入不大时,才会与感知器表现不同。
让我们看一下 sigmoid 函数和阶跃函数的图像:
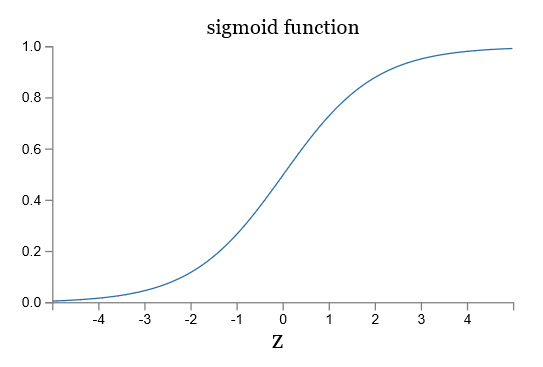
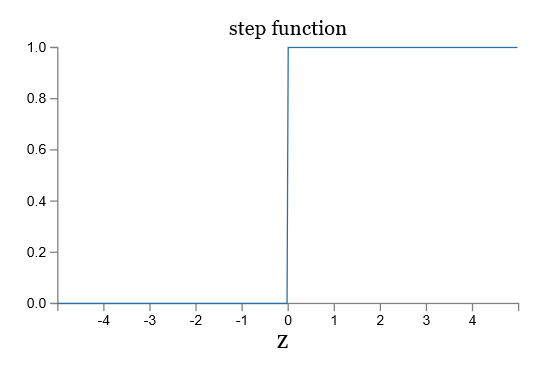
如果 $\sigma$ 是阶跃函数,那么 sigmoid 神经元就会退化成感知器,也就是说 sigmoid 神经元是平滑了的感知器。函数 $\sigma$ 的平滑度意味着,权重的微小变化 $\Delta w_j$ 和偏移的微小变化 $\Delta b$ 会在输出有相应的变化 $\Delta \mbox{output}$,运用泰勒公式可得:
\begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial , \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial , \mbox{output}}{\partial b} \Delta b, \label{5} \end{eqnarray}
其中,求和是对所有的权重和偏移变化求和。 $\partial ,\mbox{output} / \partial w_j$ 是 $\mbox{output}$ 对 $w_j$ 的偏导数,$\partial , \mbox{output} /\partial b$ 是 $\mbox{output}$ 对 $b$ 的偏导数。从这个近似表达式可以看出,$\Delta \mbox{ouput}$ 是 $\Delta w_j, \Delta b$ 的线性函数。比起感知器那种非线性的输出输入关系,线性化便于调试,也有利于算法化。
如何理解 sigmoid 神经元的输出呢?显然最大的不同是 sigmoid 神经元不只输出 0 或 1,而是 0,1 之间所有的实数,比如 0.4 来指出一幅图片是 9 的概率为 40%,60% 的概率不是 9。
神经网络的结构
神经网络的结构:
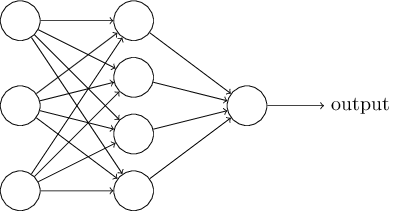
如上所述,最左边的那一层被称做输入层,其中的神经元是输入神经元。最右或者输出层包含了输出神经元,该例中只有一个输出神经元。由于中间的神经元既不是输入也不是输出,中间那层被称为隐藏层。该例中只有一个隐藏层,有些神经网络有多个隐藏层,比如下面这张图中有两个隐藏层:
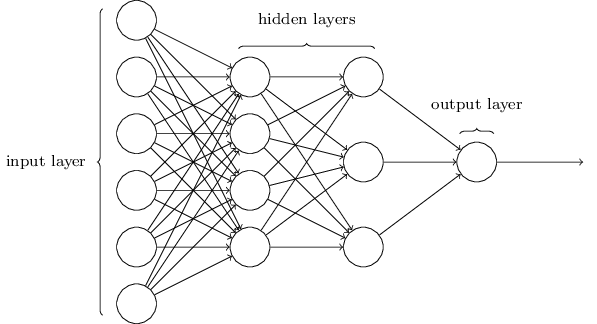
神经网络输入输出的设计通常很直接。比如手写数字,假设扫描图是 $28 \times 28=784$ 的灰度图像,输入就有 784 个神经元,输出就是每个数字的概率,一共 10 个输出神经元。